Adjacent Angles: Definitions, Properties, and Applications
Introduction
Adjacent angles are a fundamental concept in geometry that play a crucial role in various mathematical problems and real-world applications. Understanding adjacent angles involves recognizing their definitions, properties, and how they interact with other geometric figures. This comprehensive guide will delve into all aspects of adjacent angles, helping you grasp their significance and applications in mathematics and beyond.
What are Adjacent Angles?
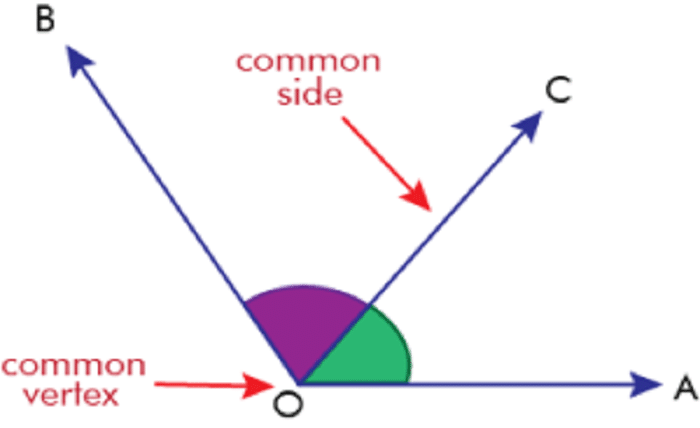
Adjacent angles are two angles that share a common vertex and a common side but do not overlap. These angles lie next to each other, forming a straight line when combined. Understanding the basic definition of adjacent angles is the first step in exploring their properties and applications.
Properties of Adjacent Angles
Adjacent angles have several key properties that make them important in geometry. One of the primary properties is that the sum of adjacent angles can vary depending on their arrangement, but they always share a common vertex and side. Another important property is that adjacent angles can form complementary or supplementary angles, depending on their measurements.
Complementary and Supplementary Adjacent Angles
Adjacent angles can be either complementary or supplementary. Complementary adjacent angles sum up to 90 degrees, while supplementary adjacent angles sum up to 180 degrees. Understanding these relationships is crucial for solving various geometric problems and proving mathematical theorems.
How to Identify Adjacent Angles
Identifying adjacent angles involves looking for angles that share a common vertex and side without overlapping. Diagrams and visual aids can be helpful in recognizing these angles. Practice with different geometric figures will enhance your ability to identify adjacent angles accurately.
Adjacent Angles in Parallel Lines
In the context of parallel lines, adjacent angles play a significant role. When two parallel lines are intersected by a transversal, the adjacent angles formed have specific relationships. These relationships help in understanding angle measures and proving geometric properties related to parallel lines and transversals.
Applications of Adjacent Angles in Geometry
Adjacent angles are used in various geometric constructions and proofs. They help in solving problems involving polygons, circles, and other geometric figures. Understanding how adjacent angles work enables you to apply them in complex geometric problems, making it easier to find solutions and understand geometric relationships.
Real-World Applications of Adjacent Angles
Adjacent angles are not limited to theoretical geometry; they have practical applications in the real world. For example, they are used in engineering, architecture, and various design fields to ensure accurate measurements and constructions. Understanding adjacent angles can help in solving real-world problems and creating precise designs.
Solving Problems Involving Adjacent Angles
Solving problems involving adjacent angles requires a good understanding of their properties and relationships. This section will provide step-by-step examples and practice problems to help you apply your knowledge of adjacent angles in various scenarios. By working through these problems, you will enhance your problem-solving skills and gain confidence in handling adjacent angles.
Common Mistakes and How to Avoid Them
When working with adjacent angles, common mistakes can occur, such as misidentifying angles or incorrect calculations. Understanding these common errors and learning how to avoid them is crucial for accurate problem-solving. This section will highlight typical mistakes and provide tips on how to avoid them.
Advanced Topics Related to Adjacent Angles
Adjacent angles connect to more advanced geometric concepts, such as angle bisectors, exterior angles, and angle pairs in polygons. Exploring these advanced topics will deepen your understanding of adjacent angles and their applications in higher-level geometry. This section will introduce these concepts and show how they relate to adjacent angles.
Teaching Adjacent Angles
Teaching adjacent angles effectively requires clear explanations, visual aids, and practical examples. This section will provide tips and strategies for educators to help students grasp the concept of adjacent angles. By using these teaching methods, you can make learning about adjacent angles engaging and accessible for students.
Conclusion:
In conclusion, adjacent angles are a fundamental concept in geometry with wide-ranging applications. Understanding their properties, identifying them accurately, and applying them in various contexts are essential skills for anyone studying mathematics. Whether in theoretical problems or real-world applications, adjacent angles play a crucial role in shaping our understanding of geometric relationships.
FAQs
Q1: What are adjacent angles?
A1: Adjacent angles are two angles that share a common vertex and a common side but do not overlap, forming a straight line when combined.
Q2: How can you identify adjacent angles?
A2: Adjacent angles can be identified by looking for angles that share a common vertex and side without overlapping, often highlighted in geometric diagrams.
Q3: What is the difference between complementary and supplementary adjacent angles?
A3: Complementary adjacent angles sum up to 90 degrees, while supplementary adjacent angles sum up to 180 degrees.
Q4: How are adjacent angles used in real-world applications?
A4: Adjacent angles are used in engineering, architecture, and design to ensure accurate measurements and constructions, solving practical problems.
Q5: What are common mistakes when working with adjacent angles?
A5: Common mistakes include misidentifying angles and incorrect calculations. Avoid these by practicing accurate identification and double-checking your work.




