45-Degree Angle: A Comprehensive Guide
Introduction
The 45-degree angle is a fundamental concept in geometry, frequently encountered in various disciplines including mathematics, engineering, and architecture. Its simplicity and versatility make it a crucial element in both theoretical studies and practical applications. In this blog post, we will delve into the properties of the 45-degree angle, its significance, and its diverse applications.
What is a 45-Degree Angle?
A 45-degree angle is one of the most easily recognizable and significant angles in geometry. It is formed when two rays diverge from a common point and create an angle of 45 degrees. This angle is exactly half of a right angle, which is 90 degrees, making it a fundamental building block in the study of angles and shapes.
Mathematical Properties of a 45-Degree Angle
In mathematical terms, a 45-degree angle has several notable properties. For instance, in a right-angled triangle, a 45-degree angle is often associated with the 45-45-90 triangle, where the two legs are of equal length, and the hypotenuse is √2 times the length of each leg. This property is frequently used in trigonometric calculations and geometric constructions.
45-Degree Angle in Trigonometry
The 45-degree angle holds a special place in trigonometry. The sine and cosine of a 45-degree angle are both equal to √2/2, while the tangent is 1. These values are fundamental in various trigonometric functions and are used to simplify complex calculations. The 45-degree angle is also used in deriving and understanding the unit circle.
Applications in Architecture
In architecture, the 45-degree angle is often utilized to create visually appealing and structurally sound designs. It can be seen in the layout of roofs, the design of certain types of windows, and in the aesthetic elements of buildings. The 45-degree angle provides a balance between visual interest and structural efficiency, making it a popular choice among architects.
Engineering and the 45-Degree Angle
Engineers frequently use the 45-degree angle in various aspects of design and construction. Whether it’s in the creation of ramps, roads, or mechanical components, the 45-degree angle is essential for ensuring stability and functionality. Its properties allow for the efficient transfer of forces and the creation of robust structures.
The Role of the 45-Degree Angle in Art
Artists also leverage the 45-degree angle to add dynamic elements to their work. Whether in painting, sculpture, or graphic design, the 45-degree angle can create a sense of movement and depth. Understanding how to use this angle effectively can enhance the composition and impact of an artwork.
45-Degree Angle in Everyday Life
The 45-degree angle is not just confined to specialized fields; it is also present in everyday life. From the way we position our monitors and desks to the way we hold our smartphones, the 45-degree angle plays a subtle but significant role. Recognizing its presence can lead to better ergonomic choices and improved comfort in daily activities.
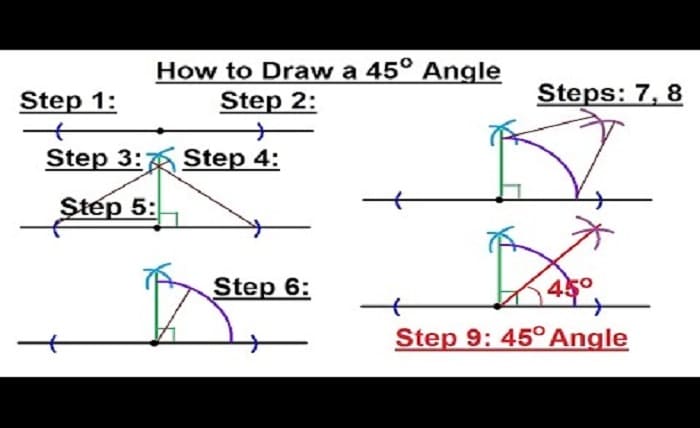
How to Calculate a 45-Degree Angle
Calculating a 45-degree angle is straightforward, especially with the help of basic geometric tools. A protractor is the most common tool used to measure and draw a 45-degree angle. Additionally, understanding the properties of right-angled triangles can simplify the process of creating this angle in various contexts.
Advanced Uses of the 45-Degree Angle
In more advanced fields such as robotics and computer graphics, the 45-degree angle is used to optimize algorithms and enhance performance. For example, in computer graphics, a 45-degree angle can help in rendering images more efficiently. In robotics, it can be used to design movements and pathways that are both efficient and effective.
Teaching the 45-Degree Angle
Teaching the concept of a 45-degree angle is an essential part of the geometry curriculum. Educators use a variety of tools and methods to help students understand and apply this angle in different scenarios. From hands-on activities to digital simulations, the goal is to make the concept of the 45-degree angle accessible and engaging.
Conclusion
The 45-degree angle is a cornerstone of geometry, with applications that span across multiple disciplines. Its simplicity, combined with its versatility, makes it an invaluable tool in both theoretical and practical contexts. By understanding the properties and uses of the 45-degree angle, one can gain deeper insights into the world of mathematics, architecture, engineering, art, and everyday life.
FAQs
1. What is the significance of a 45-degree angle in geometry?
The 45-degree angle is significant in geometry because it is half of a right angle, making it a fundamental element in the study of shapes and angles. Its properties are frequently used in various geometric constructions and calculations.
2. How is the 45-degree angle used in architecture?
In architecture, the 45-degree angle is used to create visually appealing and structurally sound designs. It is commonly seen in roof layouts, window designs, and other architectural elements that require a balance of aesthetics and functionality.
3. Why is the 45-degree angle important in trigonometry?
The 45-degree angle is important in trigonometry because its sine and cosine values are equal to √2/2, and its tangent value is 1. These values simplify many trigonometric functions and are essential in understanding the unit circle and other trigonometric concepts.
4. How can I calculate a 45-degree angle?
You can calculate a 45-degree angle using a protractor or by constructing a right-angled triangle with equal legs, which naturally forms a 45-degree angle. Understanding the properties of right-angled triangles can also aid in calculating this angle.
5. What are some advanced applications of the 45-degree angle?
Advanced applications of the 45-degree angle can be found in fields like robotics and computer graphics. In these areas, the angle is used to optimize algorithms, enhance performance, and design efficient movements and pathways.




