45 45 90 Triangles: Properties, Applications, and Solving Techniques
Introduction
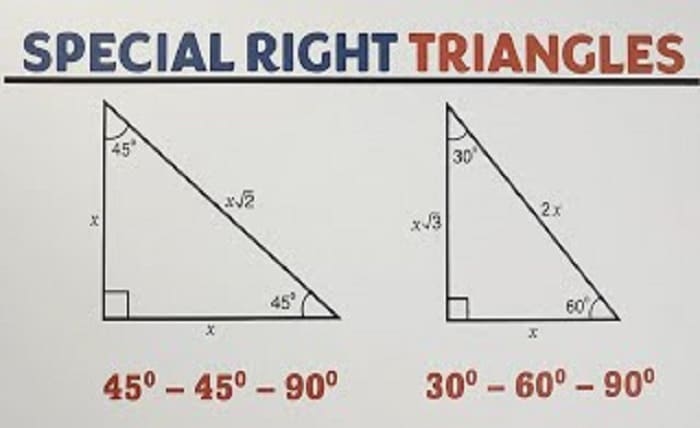
The 45 45 90 triangle is a special type of right triangle that has unique properties and applications in geometry. This triangle, known for its angles of 45 degrees, 45 degrees, and 90 degrees, is a fundamental concept in trigonometry and various fields of mathematics. Understanding the 45 45 90 triangle can simplify solving complex geometric problems and aid in practical applications.
The 45 45 90 triangle is characterized by its isosceles nature, meaning it has two sides of equal length. This equality in sides leads to consistent and predictable relationships between the sides and angles of the triangle. This blog will delve into the essential aspects of the 45 45 90 triangle, providing a thorough understanding of its properties, applications, and methods for solving problems involving this triangle.
Properties of the 45 45 90 Triangle
One of the most notable properties of the 45 45 90 triangle is the relationship between its sides. In a 45 45 90 triangle, the lengths of the two legs are equal, and the hypotenuse is 2\sqrt{2} times the length of each leg. This relationship can be expressed as:
a=ba = b c=a2c = a \sqrt{2}
where aa and bb are the legs, and cc is the hypotenuse. This predictable ratio simplifies many geometric calculations involving the 45 45 90 triangle.
Another important property is the equal angles of 45 degrees. This symmetry leads to several practical applications in construction, design, and navigation. The 45 45 90 triangle’s properties make it a versatile tool in both theoretical and applied mathematics.
Derivation of Side Lengths in a 45 45 90 Triangle
The side lengths of a 45 45 90 triangle can be derived using the Pythagorean theorem. Since the two legs are equal, we can denote each leg as aa. The hypotenuse (cc) can be found using:
c2=a2+a2c^2 = a^2 + a^2 c2=2a2c^2 = 2a^2 c=2a2c = \sqrt{2a^2} c=a2c = a \sqrt{2}
Thus, in a 45 45 90 triangle, if one leg is known, the hypotenuse can be easily calculated by multiplying the leg by 2\sqrt{2}. This derivation underscores the simplicity and utility of the 45 45 90 triangle in solving geometric problems.
Applications of the 45 45 90 Triangle in Real Life
The 45 45 90 triangle has numerous applications in real life, particularly in fields requiring precise measurements and constructions. In architecture, this triangle is used to design roofs, ramps, and other structural elements where a consistent angle and length relationship is crucial.
In navigation and surveying, the 45 45 90 triangle helps in triangulation methods to determine distances and angles. The predictability of this triangle’s properties allows for quick and accurate calculations, making it a valuable tool for engineers and surveyors.
In art and design, the 45 45 90 triangle is often employed to create symmetrical patterns and designs. Its inherent balance and proportional relationships contribute to aesthetically pleasing compositions, demonstrating its versatility beyond pure mathematics.
Solving Problems Involving the 45 45 90 Triangle
Solving problems involving the 45 45 90 triangle typically involves using its side length relationships and angle properties. For example, given one leg of the triangle, the hypotenuse can be found by multiplying the leg by 2\sqrt{2}. Conversely, if the hypotenuse is known, each leg can be determined by dividing the hypotenuse by 2\sqrt{2}.
Let’s consider an example problem: If a 45 45 90 triangle has legs of length 5 units, what is the length of the hypotenuse? Using the relationship c=a2c = a \sqrt{2}:
c=5×2≈7.07c = 5 \times \sqrt{2} \approx 7.07
Thus, the hypotenuse is approximately 7.07 units. This straightforward approach makes the 45 45 90 triangle a useful tool in geometry and trigonometry.
The Role of the 45 45 90 Triangle in Trigonometry
In trigonometry, the 45 45 90 triangle plays a significant role due to its simple and consistent angle measures. The sine, cosine, and tangent of 45 degrees are all well-defined and frequently used values:
sin(45∘)=cos(45∘)=22\sin(45^\circ) = \cos(45^\circ) = \frac{\sqrt{2}}{2} tan(45∘)=1\tan(45^\circ) = 1
These values are fundamental in solving various trigonometric problems and in the derivation of other trigonometric identities. The 45 45 90 triangle thus serves as a foundational element in the study of trigonometry.
Constructing a 45 45 90 Triangle
Constructing a 45 45 90 triangle is a straightforward process that can be done using a compass, ruler, and protractor. Here are the steps to construct a 45 45 90 triangle:
- Draw a horizontal line segment: This will be one leg of the triangle.
- Use a protractor to measure a 45-degree angle: At one end of the line segment, draw a line at a 45-degree angle.
- Draw the second leg: Measure and draw the second leg of equal length to the first.
- Complete the hypotenuse: Connect the ends of the two legs to form the hypotenuse.
By following these steps, you can accurately construct a 45 45 90 triangle, ensuring the correct proportions and angle measures.
Comparing the 45 45 90 Triangle to Other Special Triangles
The 45 45 90 triangle is one of several special triangles in geometry, each with unique properties. Another common special triangle is the 30 60 90 triangle, which has different side length relationships and angle measures. While the 45 45 90 triangle has equal legs and a hypotenuse of 2\sqrt{2} times the leg, the 30 60 90 triangle has side lengths in the ratio of 1 : 3\sqrt{3} : 2.
Comparing these triangles helps in understanding their distinct properties and applications. The 45 45 90 triangle is particularly useful for problems involving equal lengths and angles, whereas the 30 60 90 triangle is often used in problems requiring different proportions.
Advanced Applications of the 45 45 90 Triangle in Mathematics
Beyond basic geometry, the 45 45 90 triangle has advanced applications in mathematics, including calculus and complex numbers. In calculus, the triangle is used in integrating trigonometric functions and solving problems involving right-angle triangles.
In the field of complex numbers, the 45 45 90 triangle helps in visualizing complex multiplication and division. The properties of this triangle simplify the geometric representation of complex numbers, making it easier to understand their behavior in the complex plane.
Looking for the perfect Sigma PNG images to enhance your designs or projects? Our collection offers high-resolution Sigma PNG files with transparent backgrounds, ideal for logos, memes, video edits, and more. Whether you’re a designer, content creator, or student, these versatile PNGs can easily be used in presentations, thumbnails, or social media content. No need to worry about backgrounds – just download and use instantly. Stay ahead with the trend of the “Sigma male” concept and add that bold edge to your graphics. Explore and download your favorite Sigma PNG images today for free!
Conclusion
The 45 45 90 triangle is a fundamental concept in geometry and trigonometry, known for its unique properties and wide range of applications. Understanding the relationships between the sides and angles of the 45 45 90 triangle simplifies solving various mathematical problems. From basic construction to advanced applications, the 45 45 90 triangle remains an essential tool in the mathematician’s toolkit.
By mastering the properties and solving techniques of the 45 45 90 triangle, students and professionals alike can enhance their mathematical skills and apply them to real-world situations. Whether in architecture, navigation, or advanced mathematics, the 45 45 90 triangle continues to be a valuable and versatile geometric figure.
FAQs
1. What is a 45 45 90 triangle? A 45 45 90 triangle is a special right triangle with two equal angles of 45 degrees and one right angle of 90 degrees.
2. How do you find the hypotenuse of a 45 45 90 triangle? The hypotenuse is 2\sqrt{2} times the length of either leg. If one leg is known, multiply it by 2\sqrt{2} to find the hypotenuse.
3. What are the properties of a 45 45 90 triangle? The 45 45 90 triangle has equal legs and a hypotenuse that is 2\sqrt{2} times the length of each leg, with angles of 45, 45, and 90 degrees.
4. How is the 45 45 90 triangle used in real life? The 45 45 90 triangle is used in architecture, navigation, surveying, and design for its predictable proportions and angles.
5. What is the significance of the 45 45 90 triangle in trigonometry? In trigonometry, the 45 45 90 triangle helps define the sine, cosine, and tangent of 45 degrees, which are fundamental values used in various calculations.




